Symbols, Terminology and Constants in Science and Mathematics

Symbols, Terminology and Constants in Science and Mathematics

Science and Mathematics uses a large range of units, symbols and terms, and initially it can seem like a foreign language. Here we have an inexhaustive list of commonly used mathematical terms and symbols that appear commonly in all sciences – especially physical and inorganic chemistry, spectroscopy and analytical chemistry. Click on these links to jump to The Greek Alphabet – Factor Prefixes – Constants – Formulae

The Greek Alphabet

The modern alphabet on which most Western alphabets are based is a combination of the Latin and Greek alphabets. Characters from the Greek alphabet appear in most science and mathematics. They can be used to represent more than one quantity. Usually the use is specified. However, some common occurrences are listed below. NOTE: (upper) and (lower) indicate the upper case and lower case characters respectively.

Lower case	Upper case	Name	Common use
α	Α	alpha	Used as a general variable in numerous situations. Always specified. Used often in quantum mechanics.
β	Β	beta	Used as a general variable in numerous situations. Always specified. used often in quantum mechanics.
γ	Γ	gamma	An irrep in group theory (upper).
δ	Δ	delta	Indicates an infinitesimal change (lower) or general finite change (upper). Lower case is also used to signify a partial derivative.
ε	Ε	epsilon	Permitivity of free space (ε0).
ζ	Ζ	zeta	Effective nuclear charge in quantum chemistry (lower).
η	Η	eta	Used to represent many coefficients. Commonly, viscosity (lower).
θ	Θ	theta	A context-specific angle (lower), or heat (upper).
ι	Ι	iota
κ	Κ	kappa	Numerous uses. In chemistry – the compressability of a compound (lower).
λ	Λ	lambda	Wavelength (lower) of a wave or particle.
μ	Μ	mu	Symbol for “micro” (1×10-6) (lower). Also the symbol for “reduced mass” – see below.
ν	Ν	nu	Frequency, Hz or s-1 (lower)
ξ	Ξ	xi	Numerous uses. Used instead of Q for the partition function in a grand canonical ensemble in statistical mechanics (upper).
ο	Ο	omicron
π	Π	pi	Important irrational number in mathematics (lower). Mathematical operator for “product of all terms over a specified region” (upper).
ρ	Ρ	rho	Density (lower). Can be physical density (kg m-3), or some specified density, such as electron density (ρ(e–)).
σ	Σ	sigma	Numerous uses. Indicates sigma-bonds, collision cross-section etc. (lower). Mathematical operator for “sum of all terms over a specified region” (upper).
τ	Τ	tau	Some specific time not denoted by t (lower). Usually the “1/e” time.
υ	Υ	upsilon	Uncommonly used. Usage usually specified.
φ	Φ	phi	Numerous uses in the mathematics of quantum mechanics. Can indicate a specific eigenstate (lower), a general eigenstate (upper). Used in geometry to indicate an angle in the spherical polar co-ordinate system (lower).
χ	Χ	chi	The character of an irrep in group theory (upper).
ψ	Ψ	psi	Used extensively in quantum mechanics. Represents wavefunctions. Component of the Schrödinger equation. Lower case is usually a specific wavefunction, whereas upper case might be a general wavefunction.
ω	Ω	omega	Angular frequency (lower) in rotation. Unit of electrical resistance (upper). Can be adapted to be used in rotation-vibration spectroscopy (e.g ϖ, the central point between the P and Q branches in rot-vib spec.)

Factor Prefixes

Often – rather than using a number in standard mathematical form -it is preferable to use a quantity’s units, with a suitable factor prefix to indicate scale. For example, it is much quicker and more simple to write λ = 4.00×10^-7 m as 400 nm. The n, for “nano”, is a prefix used to indicate a factor of 1×10^-9.

 

Prefix	Name	Scale
E	exa	1018
P	peta	1015
T	tera	1012
G	giga	109
M	mega	106
k	kilo	103
d	deci	101
c	centi	10-2
m	milli	10-3
μ	micro	10-6
n	nano	10-9
p	pico	10-12
f	femto	10-15
a	atto	10-18
z	zepto	10-21
y	yocto	10-24

Constants

Below are listed some useful constants that are important in physical chemistry and spectroscopy.

Constant	Value	Units	Equivalency
h – Planck’s constant	6.626068×10-34	J s
ħ – reduced Planck’s constant	1.054571×10-34	J s	h / 2π
amu – atomic mass unit	1.660539×10-27	kg
kB – Boltzmann’s constant	1.380650×10-23	J K-1
R – molar gas constant	8.314472×100	J mol-1 K-1	NAkB
NA – Avogadro’s number	6.022141×1023	(atoms, particles etc.) mol-1
c – speed of light in a vacuum	2.997925×108	m s-1
me – mass of an electron	9.109382×10-31	kg
e – elementary charge	1.602177×10-19	C
ε0 – permittivity of free space	8.854188×10-12	F m-1	1 / μ0c02
μ0 – vacuum permeability	4π×10-7	J s2 / C2 m

Formulae

Below are listed some common formulae used in the theory behind basic spectroscopic techniques, divided into relevant subsections.

Basic Equations

Momentum: p = mv
Kinetic Energy: E_k = ½mv² = p²/2m

Speed of light: c = ν×λ

Energy of a wave: E = hν

de Broglie formula: λ = h/p

Boltzmann Statistics

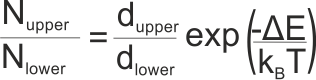
where N_upper is the population of the upper state, N_lower is the population of the lower state, d_upper and d_lower are the degeneracies of the upper and lower states, ΔE is the energy gap between the two states (in Joules, not kJ), k_B is Boltzmann’s constant and T is the absolute temperature of the system (in K)

Rotational Spectroscopy

where F(J) is the energy of rotational level J and B is the rotational constant

where h is Planck’s constant, I is the moment of inertia, c is the speed of light in vacuo, in cm s^-1

where μ is the reduced mass of the molecule

where degeneracy of a rotational energy level J is given by

The primary selection rule for pure rotational spectroscopy is

The line spacing in a pure rotation spectrum is simply given by

Vibrational Spectroscopy

The energy of a level in a vibrational system is given by

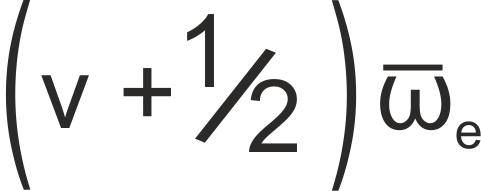
where ω_e is the harmonic band centre, given by

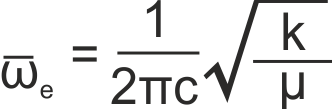
where k is the bond force constant, μ is the reduced mass of the molecule and c is the speed of light in a vacuum. The usual selection rule of Δv = ±1 applies.