Molecular rotations require little energy to excite them. Pure rotation spectra occur in the microwave region of the spectrum (~1 – 200 cm-1). It is important to note that a molecule cannot rotate about some arbitrary axis – the principle of conservation of angular momentum dictates that only a few rotations are possible. In general, rotation must be about the centre of mass of a molecule, and the axis must allow for conservation of angular momentum. In simple cases, this can often be recognised intuitively through symmetry – such as with the water molecule.
A pure rotation spectrum can only arise when the molecule possesses a permanent electric dipole moment. Like with vibrational spectroscopy, the physical effect that couples to photons is a changing dipole moment. Since molecular bond lengths remain constant in pure rotation, the magnitude of a molecule’s dipole cannot change. However, since electric dipole is a vector quantity (it has both size and direction) rotation can cause a permanent dipole to change direction, and hence we observe its spectra. Since homonuclear molecules such as dinitrogen (N2) have no dipole moment they have no rotation spectrum. Highly symmetric polyatomic molecules, such as carbon dioxide, also have no net dipole moment – the dipoles along the C-O bonds are always equal and opposite and cancel each other out. It is important to recognise also that if a molecule has a permanent dipole, but this dipole lies along the main rotation axis, then the molecule will not have a rotational spectrum – such as for a water molecule.
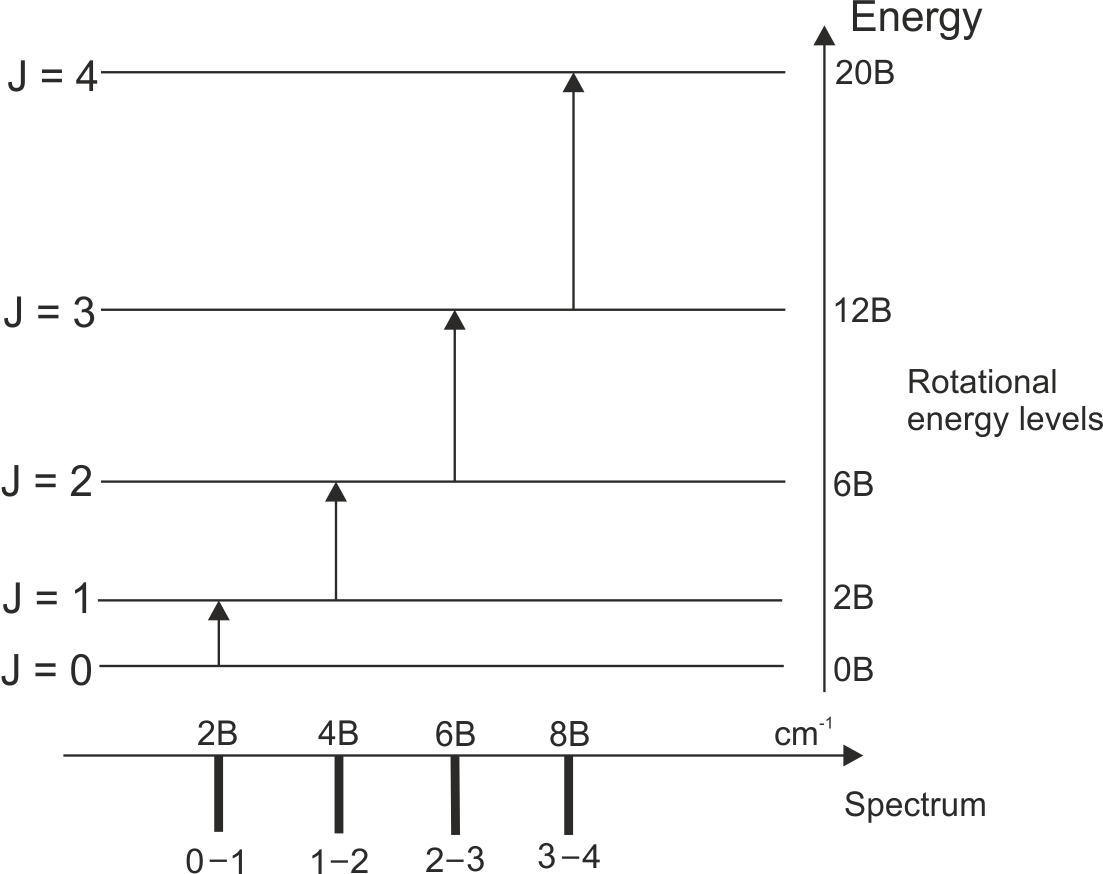
In pure rotational spectroscopy for a simple diatomic molecule, the energy levels – as displayed below – are given by EJ = BJ(J+1), where J is the rotational quantum number, B is the rotational constant for the particular molecule given by B = h2 / 8π2I with the unit of Joules, where I is the moment of inertia, given by I = μr2 – where r is the bond length of this particular diatomic molecule and μ is the reduced mass, given by μ = m1m2 / m1 + m2.
Most energy level transitions in spectroscopy come with selection rules. These rules restrict certain transitions from occuring – though often they can be broken. In pure rotational spectroscopy, the selection rule is ΔJ = ±1.
Explore examples of rotational spectroscopy of simple molecules.
Spectra
A rotational spectrum would have the following appearence. Each line corresponds to a transition between energy levels, as shown. Notice that there are no lines for, for example, J = 0 to J = 2 etc. This is because the pure rotation spectrum obeys the selection rule ΔJ = ±1. The energy gap between each level increases by 2B as the energy levels we consider increase by J = 1. This leads to the line spacing of 2B in the spectrum. Each transition has an energy value of 2B more than the previous transition.
The Molecular Dipole
The presence of a permanent molecular dipole is a requirement for a molecule being visible in rotational spectroscopy. However, it might not be immediately obvious where the dipole comes from, and what it is.
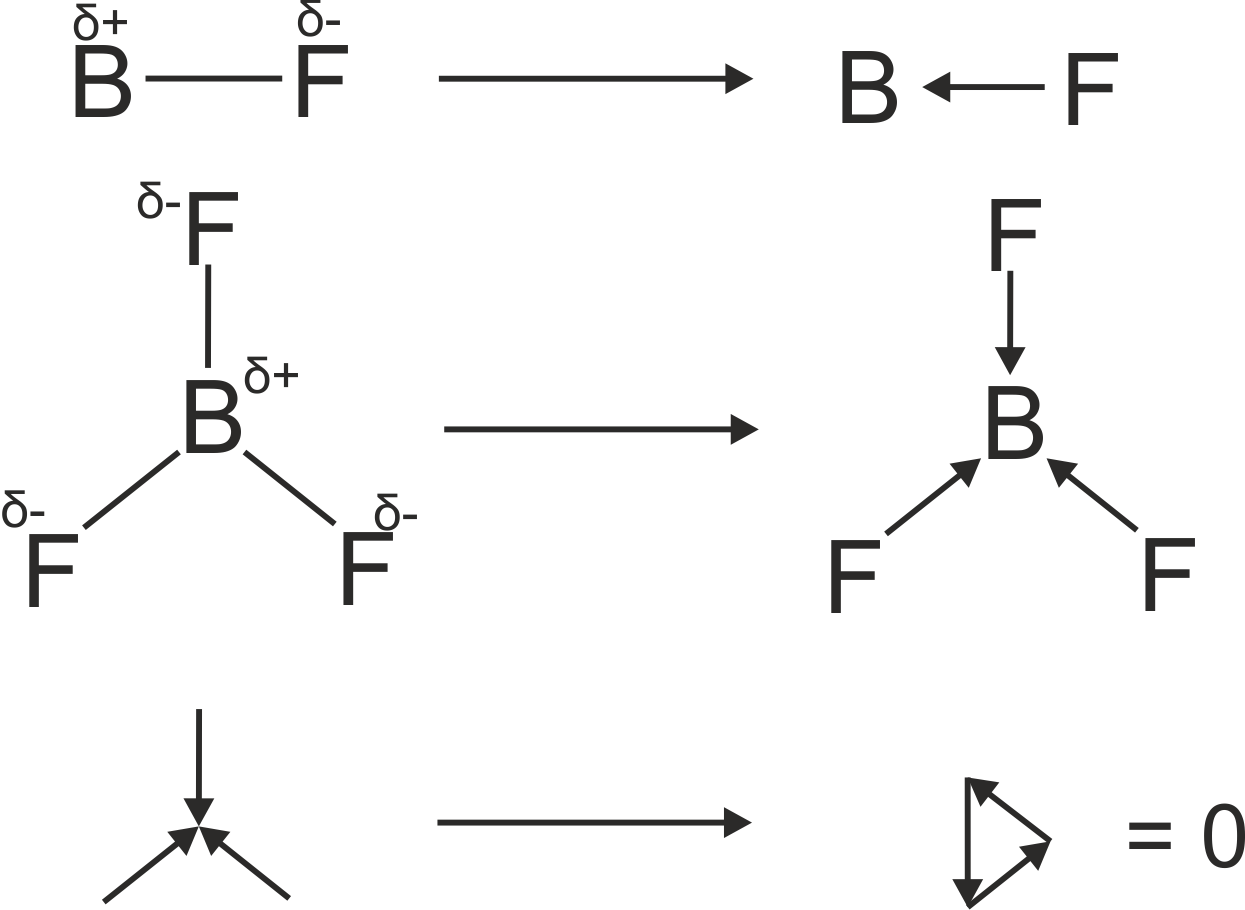
Essentially, the molecular dipole is the presence of the imbalance of charge in a molecule. The lack of an even distribution of charge leads to a potential difference between regions of the molecule. This leads to an effective, static, electric field on the molecule. It is this electric field that may couple to photons. The imbalance of charge in the molecule arises from a combination of Pauling electronegativity and molecular symmetry. For example, in BF3 (shown below), each Fluorine atom is more electronegative than the central Boron atom (3.98 and 2.04 respectively). This leads to an effective dipole moment that is positive at the central B and negative at each F. However, since the molecule is planar, and each B-F bond is of equal length, the dipoles overall cancel out. This is why boron trifluoride has no net dipole and hence no absorption in pure rotation spectroscopy. However, it does have a transient dipole in its asymmetric vibrational modes – which appear in its vibrational spectrum. You can explore molecular dipoles.
A simple example of a molecule with a permanent molecular dipole is water, shown below. In this example, the vector sum of the bond dipole moments does not equal 0, as in BF3.
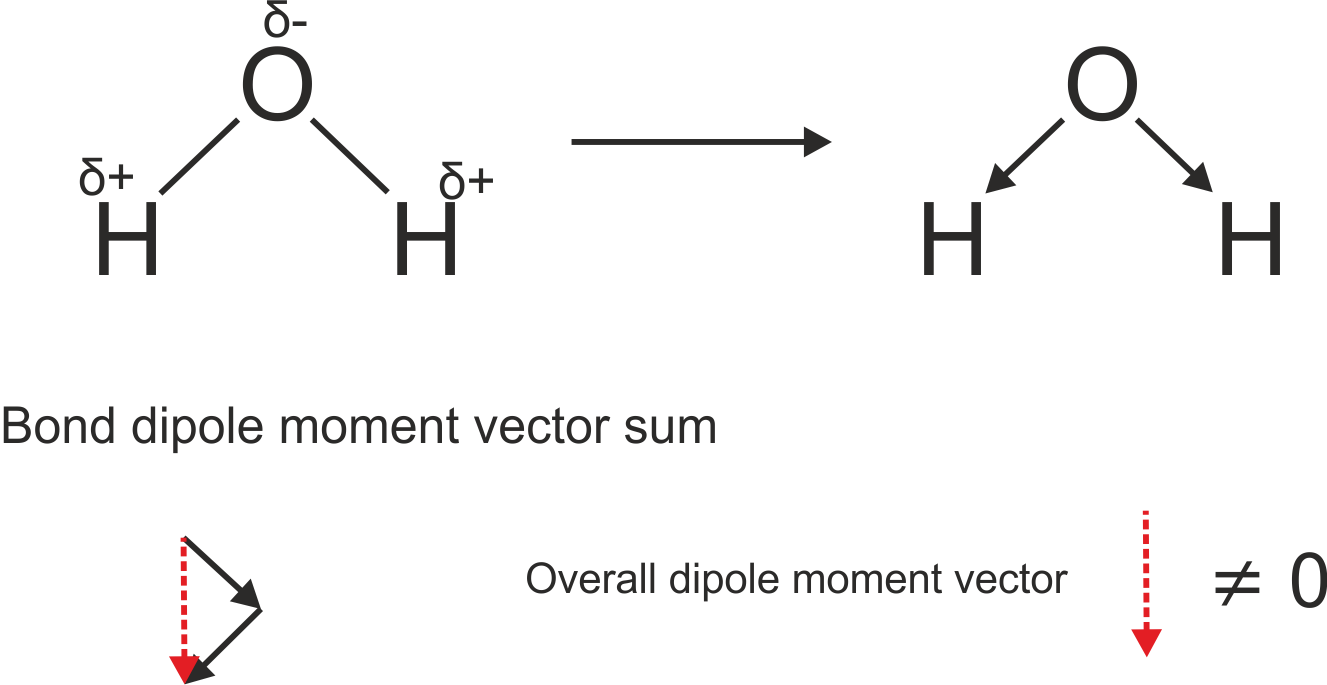
Water has a permanent molecular dipole, and so could appear in pure rotation spectroscopy. However, since this dipole vector contains the main rotation axis of the molecule, the molecular dipole remains static as the molecule rotates. As such, water does not have a pure rotation spectrum.